- vector = magnitude(크기) + direction(방향)
| 5mph (시속 5마일) | - magnitude - 속력(speed)은 scalar 값임 |
| 5mph, east | - 속도(velocity) -> vector |

- 실수좌표공간 (Real coordinate space)
- 튜플(tuple)


- 크기는 없고 방향은 정해지지 않은 영벡터를 포함한 모든 2-tuple에 대해 벡터들을 조합해 2차원 실수좌표공간도 만들어낼 수 있음 -> 이게 바로 R^2
- 마찬가지로 R^3는 모든 가능한 실수 값을 가지는 3-tuple로


(벡터의 덧셈, 벡터와 스칼라 곱셈은 쉬우니까 생략)
- 단위 벡터 (unit vector) : 길이가 1인 벡터/ [0,1], [1,0]

단위 벡터 구하는 방법:


- 직선의 매개변수

- 집합 S는 동일선상에 존재하는 벡터의 집합
- v벡터를 위치 벡터(position vector)로 보고 S집합을 수많은 위치벡터로 표현한다면 (아래와 같이) 직선에 표현됨

- v벡터는 기울기(slope) 벡터


- 크기와 방향에서 성분얻기
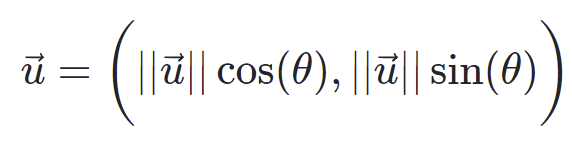
'전공공부 > 선형대수학' 카테고리의 다른 글
| [선형대수학] 선형결합 & 선형종속 (0) | 2022.07.15 |
|---|