경사하강법 기반 선형회귀 알고리즘, 확률적 경사하강법

출처: 네이버 부스트코스 인공지능(AI) 기초 다지기 3. 기초 수학 첫걸음

<목차>
1. 경사하강법 기반의 선형회귀 알고리즘
 - 경사하강법으로 선형회귀 계수 구하기
- 경사하강법 기반 선형회귀 알고리즘

2. 딥러닝에서 경사하강법의 한계

3. 확률적 경사하강법(stochastic gradient descent)
- 원리: 미니배치 연산
- 원리: 하드웨어

 

경사하강법 기반의 선형회귀 알고리즘

무어-펜로즈 역행렬을 활용한 선형회귀분석 <-> 선형 모델 외에도 적용 가능한 경사하강법-선형회귀분석 

 

---

경사하강법으로 선형회귀 계수 구하기

• 선형 회귀의 목적식은 ||y-Xβ||2 이고 이를 최소화 하는 β를 찾아야 하므로 다음과 같은 그레디언트 벡터를 구해야한다

목적식을 beta로 미분

 

주어진 beta 내에서 k번째 계수에 해당하는 beta k를 가지고 목적식을 편미분

 

* n개의 data를 가지고 계산되는 L2이기 때문에 1부터 n까지 제곱근 더해준 다음에 n으로 나누어 평균값을 구해야함

 복잡한 계산이지만 사실 Xβ를 계수 β에 대해 미분한 결과에 X^T만 곱해지는 것 

 

d차원 벡터(베타)에 대한 그레디언트 벡터를 구하는 계산

• 이제 목적식을 최소화하는 β를 구하는 경사하강법 알고리즘은 다음과 같다

t번째에서 위에서 구한 gradient vector을 빼준다 /&nbsp;람다: 수량속도

 

 

L2 노름의 제곱근이 아닌 제곱을 사용해 목적식 최소화

---

경사하강법 기반 선형회귀 알고리즘

'''
Input: X, y, lr, T, Output: beta
'''
# norm: L2-노름을 계산하는 함수
# lr: 학습률, T: 학습횟수
for t in range(T): #종료조건을 일정학습횟수로 변경한 점만 빼고 앞에서 배운 경사하강법 알고리즘과 같다
 error = y - X @ beta #∇β∥y − Xβ∥22 항을 계산해서 β를업데이트한다
 grad = - transpose(X) @ error
 beta = beta - lr * grad

 이제 경사하강법 알고리즘으로 역행렬을 이용하지 않고 회귀계수를 계산할 수 있다
 그러나 경사하강법 알고리즘에선 학습률과 학습횟수가 중요한 hyperparameter가 된다

 

경사하강법 알고리즘을 이용해 선형모델로 데이터를 생성하고 계수를 찾기

([1,2] 계수이고 y절편은 3)

import numpy as np
import sympy as sym
from sympy.abc import x
from sympy.plotting import plot

X = np.array([[1,1], [1,2], [2,2], [2,3]])
y = np.dot(X, np.array([1,2])) + 3

beta_gd = [10.1, 15.1, -6.5] #[1,2,3]이 정답
X_ = np.array([np.append(x, [1]) for x in X]) #intercept 항 추가

for t in range(5000):
    error = y- X_ @beta_gd
    #error = error/ np.linalg.norm(error)
    grad =- np.transpose(X_) @error
    beta_gd = beta_gd - 0.01 * grad

print(beta_gd)    
#[1.00000367 1.99999949 2.99999516]

---

딥러닝에서 경사하강법의 한계

• 이론적으로 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장됨
• 특히 선형회귀의 경우 목적식 ||y-Xβ||2 은 회귀계수 β에 대해 볼록함수이기 때문에 알고리즘을 충분히 돌리면 수렴이 보장됨

 

• 하지만 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로 수렴이 항상 보장되지는 않음

---

경사하강법의 단점을 보완하는 확률적 경사하강법(stochastic gradient descent)

• 모든 데이터를 사용해서 업데이트하는 대신 데이터 한 개(SGD) 또는 일부(mini batch)를 활용해 업데이트
• 볼록이 아닌(non-convex) 목적식은 SGD를 통해 최적화

 

• SGD는 데이터의 일부를 가지고 parameter를 업데이트하기 때문에 연산자원을 좀 더 효율적으로 활용하는데 도움이 됨

---

확률적 경사하강법의 원리: 미니배치 연산

• 전체 데이터 D= (X, y)를 가지고 목적식의 그레디언트 벡터인 ∇θL(D, θ)를 계산
• ∇θL(D, θ) : 현재 주어진 parameter θ에서 주어진 목적식 최소점으로 향하는 방향을 안내

 

일부를 가지고

 

목적식 모양이 달라짐

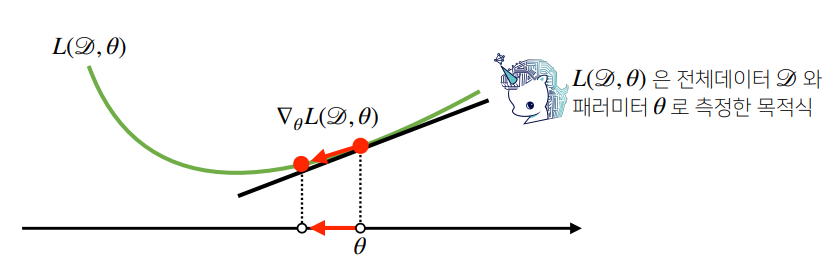
non convex 함수라도 최소점 찾을 수 있는 이유: 서로 다른 미니배치를 사용해서 곡선 모양이 바뀜. 설사 local point에 도달하더라도 극소점이 더 이상 아니게 되므로 탈출 가능.

• SGD는 볼록이 아닌 목적식에서도 사용 가능하므로 경사하강법보다 머신러닝 학습에 더 효율적임

mini batch가 빠르게 최소점 도달/ SGD에서 mini batch를 작게 잡으면 경사하강법보다 느릴 수 있음

 

---

확률적 경사하강법의 원리: 하드웨어

일반적인 경사하강법 (문제)

 

확률적 경사하강법(해결)