출처: 구름 알고리즘 먼데이 챌린지 7주차
문제
"발 없는 말이 천 리 간다"는 옛말이 있듯, 한 번 퍼져나가기 시작한 소문은 막을 수 없이 퍼져나간다.
구름이는 N명의 친구가 있고, 그 친구들 중에는 M쌍의 친구 관계가 있다. 구름이가 만약 어떤 친구에게 소문을 퍼뜨리게 된다면, 그 소문은 친구의 친구, 친구의 친구의 친구... 를 타고 퍼져나갈 것이다.
구름이가 1번 친구에게 소문을 퍼뜨렸을 때, 그 소문을 듣게 될 친구가 몇 명이나 될지를 구해보자.
예제 설명
첫 번째 예시의 친구 관계는 아래 그림과 같다.
모든 친구가 친구 관계로 연결되어 있으므로, 1번 친구에게 비밀을 전달하게 되면 모든 친구에게 비밀이 퍼져나가게 된다.
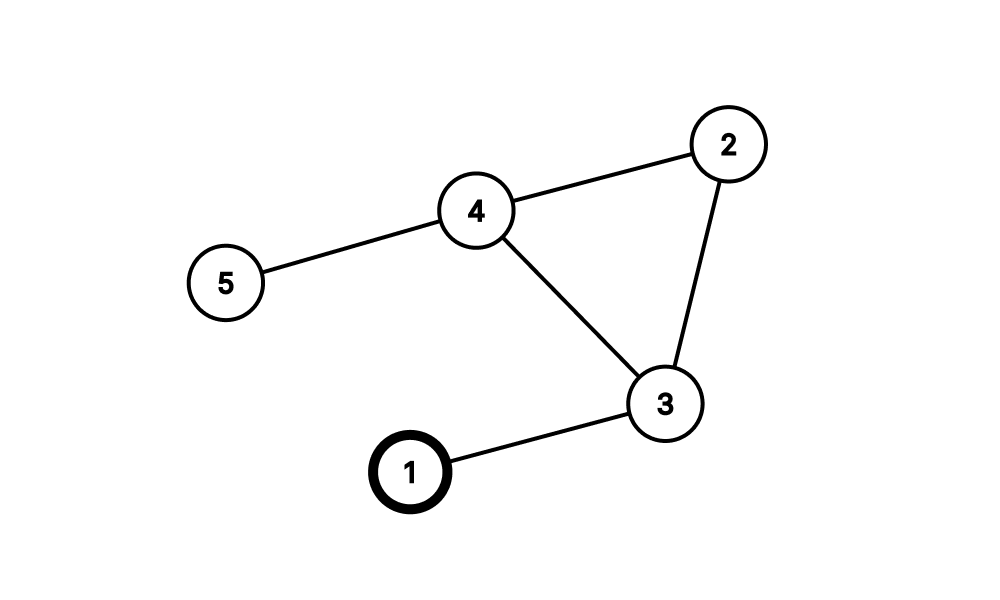
두 번째 예시의 친구 관계는 아래 그림과 같다.

1번 친구에게 비밀을 전달하게 되면 3,4,5 번 친구에게 비밀이 퍼져나가게 된다. 따라서 1번 친구를 포함해 네 명의 친구가 소문을 듣게 된다.
입력
첫 번째 줄에는 구름이의 친구의 수 N (1<=N<=500)이 주어진다. 모든 친구는 1번부터 N번까지 번호가 붙어 있다.
두 번째 줄에는 친구 관계의 수 M (1<=M<=1,000)이 주어진다.
다음 M개의 줄에는 u, v (1<= u, v <= N, u!=v) 가 공백으로 구분되어 주어진다. 모든 친구 관계는 양방향이고, 같은 친구 관계가 중복으로 주어지지 않는다.
입력에서 주어지는 모든 수는 정수이다.
출력
구름이가 1번 친구에게 소문을 냈을 때, 소문을 듣게 되는 친구의 수를 출력한다
| 입력 | 출력 | |
| 5 5 1 3 2 3 3 4 4 5 4 2 |
5 |  |
| 7 5 1 4 3 5 7 6 1 5 4 3 |
4 |  |
풀이
처음 접근법은 "서로소 집합을 활용한 사이클 판별"이었음
하지만 1번노드에서 각 노드까지 연결이 가능하냐가 핵심이지, 사이클을 찾는 문제가 아님!
모든 경우를 구해야 하므로 DFS
'''
N 명의 친구(1~N번)와 M 쌍의 친구 관계 (양방향 친구)
1번 친구한테 소문을 퍼뜨렸을 때 소문을 듣게 될 친구가 몇 명?
'''
#import sys
#sys.stdin = open('./quiz/input2.txt', 'r')
N = int(input())
M = int(input())
graph = [[] for _ in range(N + 1)] # 인접 리스트
node = [0 for _ in range(N + 1)] # 각 노드가 1과 연결되어있으면 1, 아니라면 0(인덱스 값이 노드 번호)
for _ in range(M):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
#print(graph) #[[], [3], [3, 4], [1, 2, 4], [3, 5, 2], [4]]
def DFS(n):
for next in graph[n]:
if node[next]: # 이미 방문했다면 pass
continue
node[next] = 1
DFS(next)
node[1] = 1
DFS(1)
#print(node) # [0, 1, 1, 1, 1, 1]
print(sum(node))Tip! node를 True, False로 해서 True의 개수를 세지 않고 1, 0 으로 해서 sum으로 간단히 노드의 개수를 구함
📝
인접리스트 선언
graph = [[] for _ in range(N + 1)] # N은 노드의 개수
참고: DFS로 하나의 노드에서 출발해서 갈 수 있는 노드 찾기(그래프 탐색)
(1) 각 노드별로 방문 여부를 저장하는 리스트와 (2) 노드 간 연결 정보를 담은 연결리스트가 필요하다
연결된 노드들 중 방문하지 않은 노드를 방문
visited = [False]*9 # 각 노드별 방문 여부 저장
graph = [ # 연결리스트
[],
[2,3,8],
[1,7],
[1,4,5],
[3,5],
[3,4],
[7],
[2,6,8],
[1,7]
]
stack = [] # 방문 노드 순서대로 저장
def DFS(v):
visited[v] = True
stack.append(v)
for i in graph[v]:
if not visited[i]:
DFS(i)
DFS(1)
print(stack)

'코테 공부 > 그 외 사이트' 카테고리의 다른 글
| [Python] 1206. [S/W 문제해결 기본] 1일차 - View (0) | 2022.11.25 |
|---|---|
| [Python/BFS] 3.구름이의 여행 2 (0) | 2022.11.22 |
| [Python] 1.UXUI 디자이너/ lambda, sorted (0) | 2022.11.21 |
| [Python/BFS] 이코테 미로탈출 (중요. 기본기) (0) | 2022.08.17 |
| [python/그리디] 큰 수의 법칙 (0) | 2022.08.16 |