<목차>
1. 다익스트라 알고리즘
2. 다익스트라 heap을 사용해 구현하기
3. 플로이드 워셜 알고리즘
4. 플로이드 워셜 구현하기
* 인접 행렬 VS 인접 리스트
다익스트라 알고리즘 (dijkstra)
그래프에 여러 개의 노드가 있을 때, 특정 노드에서에서 출발해 다음 노드로 가는 각각의 최단 경로를 구하는 알고리즘이다.
단, '음의 간선(0보다 작은 값을 가지는 간선)'이 없어야 한다.
다익스트라는 매번 '가장 비용이 적은 노드'를 선택하고, 임의의 과정을 반복하기 때문에 그리디 알고리즘으로 분류된다.
다익스트라는 '현재 노드에서 각 노드에 대한 최단 거리' 정보를 1차원 리스트에 저장하며 리스트를 계속 갱신해 나간다. 이 리스트가 '최단 거리 테이블'이다. 즉, 현재 처리하고 있는 노드와 인접한 노드로 도달하는 더 짧은 경로를 찾으면 이를 갱신해준다.
1. 출발 노드를 설정한다
2. 최단 거리 테이블을 초기화한다.
3. 방문하지 않은 노드 중에서 최단 거리가 짧은 노드를 선택한다.
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 계산한다.
5. 3,4번을 반복한다.
예를 들어 아래와 같은 그래프가 있을 때를 살펴보자
초기 상태에서는 다른 모든 노드로 가는 최단 거리를 '무한'으로 초기화한다.
파이썬에서 지수표기법으로 사용하는 1e9는 10억으로, 파이썬에서는 실수 자료형으로 이를 처리한다.
따라서 모든 간선이 정수형으로 표시되는 문제에서는 int(1e9)를 사용한다.
[침고] 아래 그림에서 계산한 간선은 ---- 화살표로 표시한다.







다익스트라 알고리즘 구현하기
heapq를 사용하면 최악의 경우에도 시간복잡도 O(ElogV)를 보장할 수 있다. (V는 노드의 개수, E는 간선의 개수)
왜냐하면 heapq를 사용하면 매번 최단 거리 테이블을 선형적으로 (모든 원소를 앞에서부터 하나씩) 탐색할 필요 없이
최단 거리가 가장 짧은 노드를 바로 찾을 수 있기 때문이다.
(PriorityQueue도 heapq가 가진 우선순위 큐 기능을 지원하나 일반적으로 heapq가 더 빠르다)
| 우선순위 큐 구현 방식 | Insert time complexity | Delete time complexity |
| List | O(1) | O(N) |
| Heap | O(logN) | O(logN) |
간선의 개수 E가 시간복잡도에 관여하는 이유는 큐에서 꺼낸 노드를 탐색할 때 해당 노드와 연결된 노드들만 탐색하므로
최악의 경우라도 총 간선의 개수인 만큼을 반복하게 된다.
| 노드의 수 (n) | 간선의 수(m) | 노드 정보(info) [노드1, 노드2, cost] : 노드1과 노드2 사이의 거리는 cost이다 |
| 6 | 11 |
1 2 2
1 3 5 1 4 1 2 3 3 2 4 2 3 2 3 3 6 5 4 3 3 4 5 1 5 3 1 5 6 2 |
📝
graph는 노드 간의 거리를 확인하기 위한 2차원 리스트(인접 리스트)이고,
heap은 노드를 이동하며 start_node부터 end_node까지의 최단 거리를 찾는 task를 수행하기 위한 힙이다.
graph가 [ [],
[1번 노드와 연결된 노드 번호, 해당 노드와 1번노드 간의 거리],
[2번 노드와 연결된 노드 번호, 해당 노드와 2번노드 간의 거리] , ....
[n번 노드와 연결된 노드와 n번 노드 간의 거리, 몇 번 노드인지]
] 를 담고 있다.
위 예시에서 graph는 아래와 같다.
[
[],
[(2, 2), (3, 5), (4, 1)] , # 1번 노드
[(3, 3), (4, 2)] ,
[(2, 3), (6, 5)] ,
[(3, 3), (5, 1)] ,
[(3, 1), (6, 2)] ,
[] # n번 노드
]
📝
heap에는 [new_node와 현재 노드의 거리, 현재 노드와 연결된 노드(new_node)] 를 push해준다
[new_node, new_node와의 거리] 가 아닌 이유는 거리를 기준으로 최솟값을 pop해야 하기 때문이다.
우선, heap에 시작 노드에 관한 정보인 (0, start_node)를 삽입하고,
distance[start_node]로 distance에 방문한 노드에 대한 정보 기록을 시작한다.
while문을 도는 순간 heap에는 현재 노드에 관한 정보가 들어가 있고, 현재 노드가 처리된 적이 없다면 연결된 인접 노드를 확인해서 갱신한다.
import sys
import heapq
input = sys.stdin.readline
n, m = map(int, input().split())
start = int(input())
INF = int(1e9)
distance = [INF] * (n+1)
graph = [[] for _ in range(n+1)]
for _ in range(m):
node1, node2, cost = map(int, input().split())
graph[node1].append((node2, cost)) # 위 문제는 한방향 화살표지만
#graph[node2].append((node1, cost)) # 만약 양방향이라면
def dijkstra(start):
q = []
heapq.heappush(q, (0, start)) # 시작노드로 가기 위한 최단 경로는 0으로 설정
distance[start] = 0 # 시작노드->시작노드 거리 기록
while q:
dist, node = heapq.heappop(q) # 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
if distance[node] < dist: # 현재 노드가 이미 처리된 적 있다면 무시
continue
for next in graph[node]: # 현재 노드와 연결된 노드 확인
# graph[node1] = (node2, cost) / next = [node2, cost]
cost = distance[node] + next[1] # 현재 노드를 거쳐 다른 노드로 이동하는 거리가 더 짧을 경우
if cost < distance[next[0]]: # 갱신
distance[next[0]] = cost
heapq.heappush(q, (cost, next[0]))
dijkstra(start)
for i in range(1, len(distance)):
if distance[i] == INF:
print('도달할 수 없음')
else:
print(distance[i])플로이드 워셜 (floyd-warshall)
| 다익스트라 | 플로이드 워셜 |
| 한 지점에서 다른 특정 지점까지의 최단 경로를 구한다 | 모든 지점에서 다른 모든 지점까지의 최단 경로를 구한다 |
| 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다. 그리고 해당 노드를 거쳐 가는 경로를 확인하며, 최단 거리 테이블을 갱신하는 방식으로 동작한다. | 단계마다 '거쳐 가는 노드'를 기준으로 알고리즘을 수행한다. Dab = min(Dab, Dak + Dkb) 하지만 매번 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다. |
| heapq 사용시 O(ElogV) | O(n^3) |
| 출발 노드가 한 개이므로 다른 모든 노드까지의 최단 거리를 저장하기 위해 1차원 리스트를 사용 | 2차원 리스트에 최단 거리 정보 저장 인접 행렬을 사용한다 |
| 그리디 알고리즘 | DP 알고리즘 노드의 개수 N번만큼의 단계를 반복하면서 '점화식에 맞게' 2차원 리스트를 갱신해 나간다 |
예를 들어 아래와 같은 그래프가 있을 때를 살펴보자
초기의 테이블을 만들 때는 연결된 간선에 단순히 그 값을 채우고, 연결되지 않는 간선 (ex. 1->3)은 무한으로 설정한다. 자기 자신으로 가는 경우(대각선)는 0으로 설정한다.



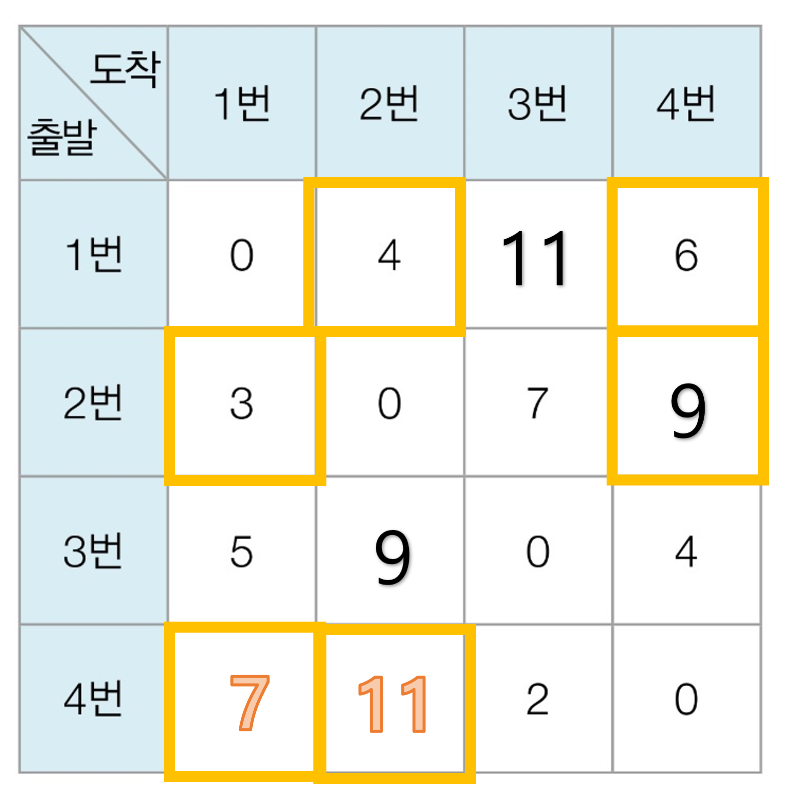
1번 노드를 거쳐 가는 경우를 생각해보자 (가장 우측 사진). 테이블이 아래와 같이 갱신된다.
고려했던 노드는 병아리색 네모로, 변경된 최소 거리 값은 주황색으로 표시했다.


(우측 사진) 이제 2번 노드를 거쳐 가는 경우를 고려하자
(좌측) 이제 3번 노드를 거쳐 가는 경우를 고려하자 (우측) 마지막으로 4번 노드를 거쳐 가는 경우를 고려하자

플로이드 워셜 구현하기
| 노드의 수 (n) | 간선의 수(m) | 노드 정보(info) [노드1, 노드2, cost] : 노드1과 노드2 사이의 거리는 cost이다 |
| 4 | 7 |
[[1, 2, 4],
[1, 4, 6], [2, 1, 3], [2, 3, 7], [3, 1, 5], [3, 4, 4], [4, 3, 2]] |
INF = int(1e9)
def solution(n, m, info):
graph = [[INF]*(n+1) for i in range(n+1)]
# 자기 자신으로 가는 비용 0으로 초기화
for a in range(1, n+1):
for b in range(1, n+1):
if a==b:
graph[a][b] = 0
# 간선 정보 입력받기
for node1, node2, cost in info:
graph[node1][node2] = cost
#graph[node2][node1] = cost # 양방향이라면
# 플로이드 워셜 수행
for k in range(1, n+1):
for a in range(1, n+1):
for b in range(1, n+1):
graph[a][b] = min(graph[a][b], graph[a][k]+ graph[k][b])
# 수행 결과 출력
for a in range(1, n+1):
for b in range(1, n+1):
if graph[a][b] == INF: # 도달할 수 없는 경우
print("INFINITY", end = " ")
else: # 도달할 수 있는 경우
print(graph[a][b], end = " ")
print()
'''
0 4 8 6
3 0 7 9
5 9 0 4
7 11 2 0
'''인접 행렬 VS 인접 리스트


인접행렬: 이차원 리스트
graph[a][b] : 노드 a에서 b를 가는 간선이 있다면 1, 아니면 0
(장점) 구현이 쉽다. 두 노드의 간선 존재 여부를 바로 알 수 있다. 두 정점 i, j의 직접 연결을 확인할 때 O(1)이 필요
(단점) 1. 간선의 개수에 비해 node의 개수가 많은 경우, 탐색이 비효율적이다 2. 공간복잡도가 O(N^2)
인접리스트: 각 노드에 연결된 노드를 원소로 가지는 리스트이다.
graph[a] 에는 a와 연결된 노드가 있다 (정점 i에 대해 i와 연결된 모든 정점을 리스트 형태로 기록합니다.)
(장점) 1. 어떤 노드의 인접한 노드를 바로 찾을 수 있다. 2. 공간복잡도가 O(N)
(단점) 연결 여부를 확인하는 게 느리다. 두 정점 i, j의 직접 연결을 확인할 때 O(N)이 필요

'코테 공부 > 코테 전략&팁' 카테고리의 다른 글
| 서로소 집합을 활용한 사이클 판별(같은 팀인지 파악) (0) | 2022.08.19 |
|---|---|
| [꿀팁] 상하좌우 이동 (0) | 2022.08.02 |
| [꿀팁] 2차원 배열 선언하기 (0) | 2022.08.02 |
| [꿀팁] 입력 값을 변수 두 개에 저장하기 (0) | 2022.08.02 |
| [꿀팁] Python 2차원 배열 회전 (0) | 2022.07.01 |