전공공부/인공지능

부스트코스 인공지능(AI) 다지기 -7 : 행렬

prefer_all 2022. 7. 19. 16:47

출처: 네이버 부스트코스 인공지능(AI) 기초 다지기 3. 기초 수학 첫걸음

<목차>
1. 행렬이란
- 행벡터, 열벡터
2. 행렬 곱셈
- @
3. 행렬 내적
- np.inner
4. 행렬 제대로 이해하기
- 벡터 공간에서 사용되는 연산자
5. 역행렬
- np.linalg.pinv()
6. 유사 역행렬, 무어펜로즈 역행렬
- 응용: 연립방정식 풀기, 선형회귀분석

 

 

행렬(matrix) 이란

  • 벡터를 원소로 가지는 2차원 배열. 행과 열이라는 index를 가짐. 
  • numpy에서는 행row 가 기본 단위임
  • 특정 행을 고정하면 행벡터라고 부름 / 특정 열을 고정하면 열벡터라고 부름
  • 벡터가 공간에서 한 점을 의미한다면 행렬은 여러 점들을 나타냄
  • 행렬의 행벡터 Xi는 i번째 데이터를 의미함. 행렬의 Xij는 i번째 데이터의 j번째 변수 값을 말함.

 

 

  • 마찬가지로 행렬끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있음. 성분곱과 스칼라곱도 벡터와 똑같음.

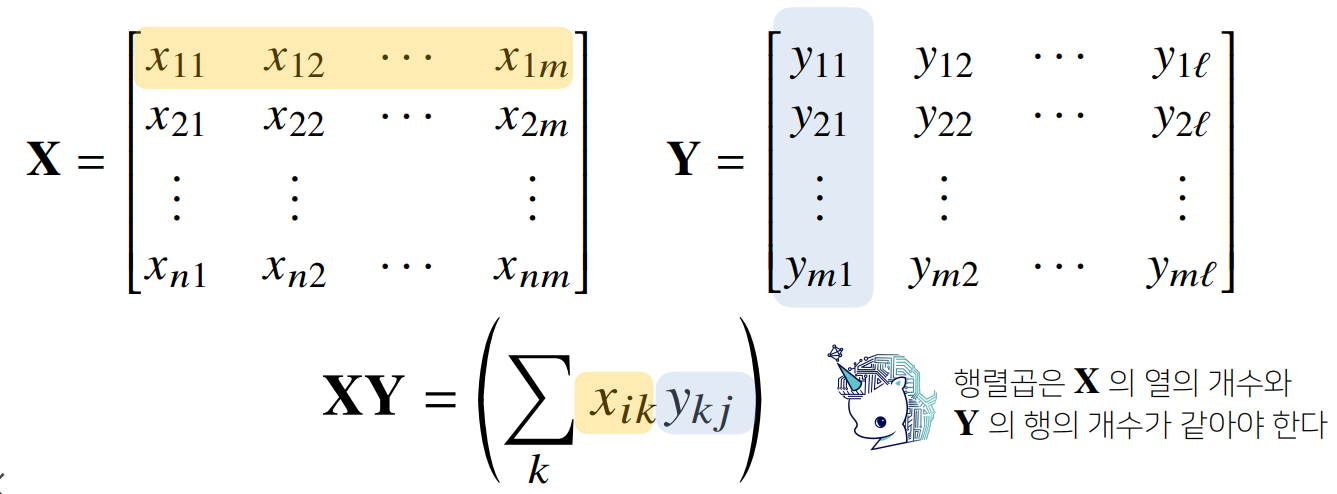
행렬 곱셈(matrix mulitiplication)  @

i 번째 행벡터와 j 번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산

 

 

x= np.array([[1,-2,3],
            [7,5,0],
            [-2, -1, 2]])

y= np.array([[0,1],
            [1, -1],
            [-2,1]])

x @ y
'''
array([[-8,  6],
       [ 5,  2],
       [-5,  1]])
-8 = 1*0+ (-2)*1 + 3*(-2)       
'''

행렬에도 내적이 있을까?

np.inner은 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산

x의 행의 개수와 y의 행의 개수가 같아야함

x= np.array([[1,-2,3],
            [7,5,0],
            [-2, -1, 2]])

y= np.array([[0,1,-1],
            [1,-1,0]])

np.inner(x, y)
'''
array([[-5,  3],
       [ 5,  2],
       [-3, -1]])
-5 = 1*0 + (-2)*1 + 3*(-1)       
'''

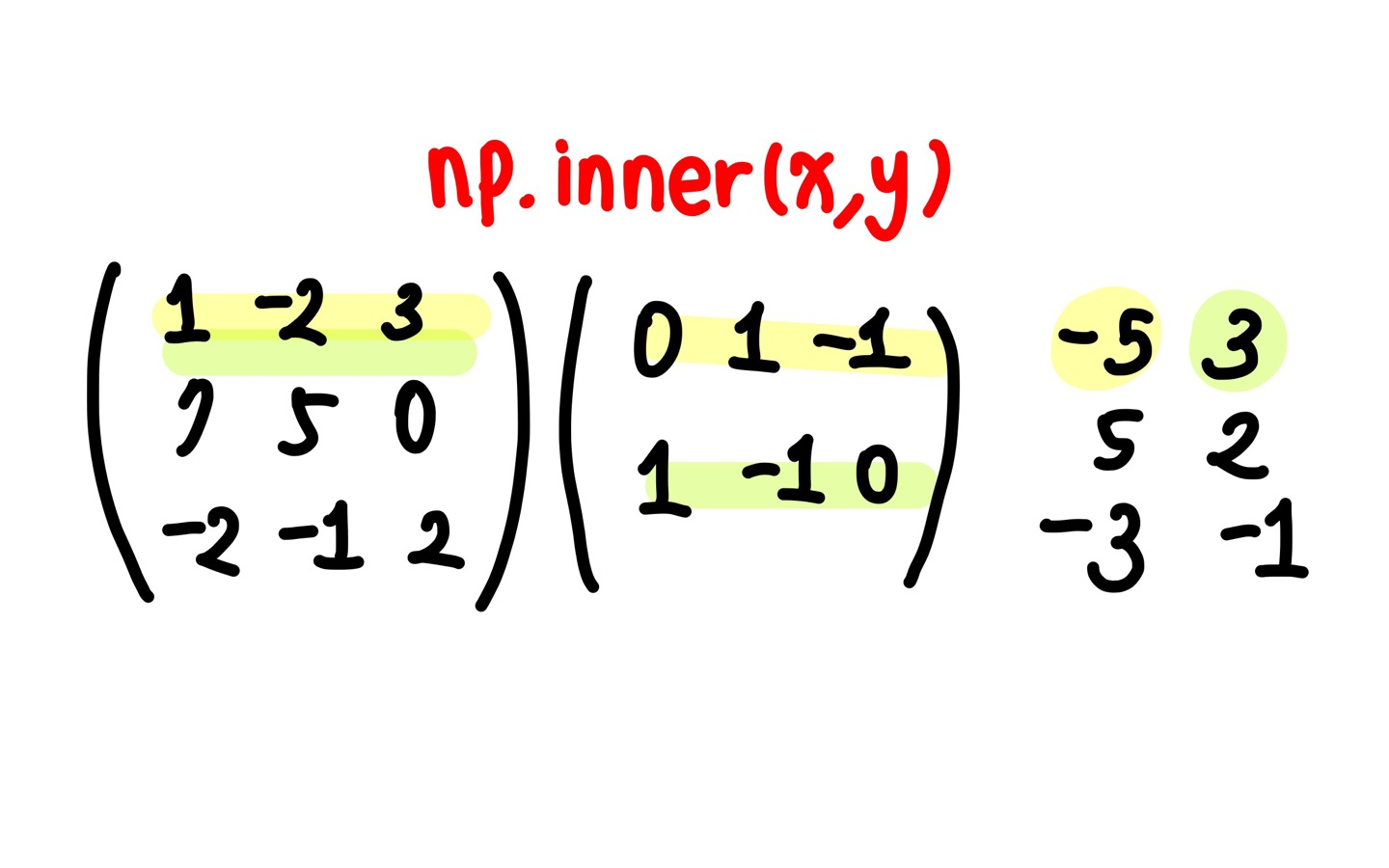
행렬 이해하기

  • 벡터 공간에서 사용되는 연산자 (operator) / 두 벡터를 연결하는, 다른 차원으로 매핑하는
  • 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있음
  • 행렬곱을 통해 패턴을 추출할 수 있고 데이터를 압축할 수 있음

 

m차원 공간의 x와 n차원 공간의 z를 연결시킴

 

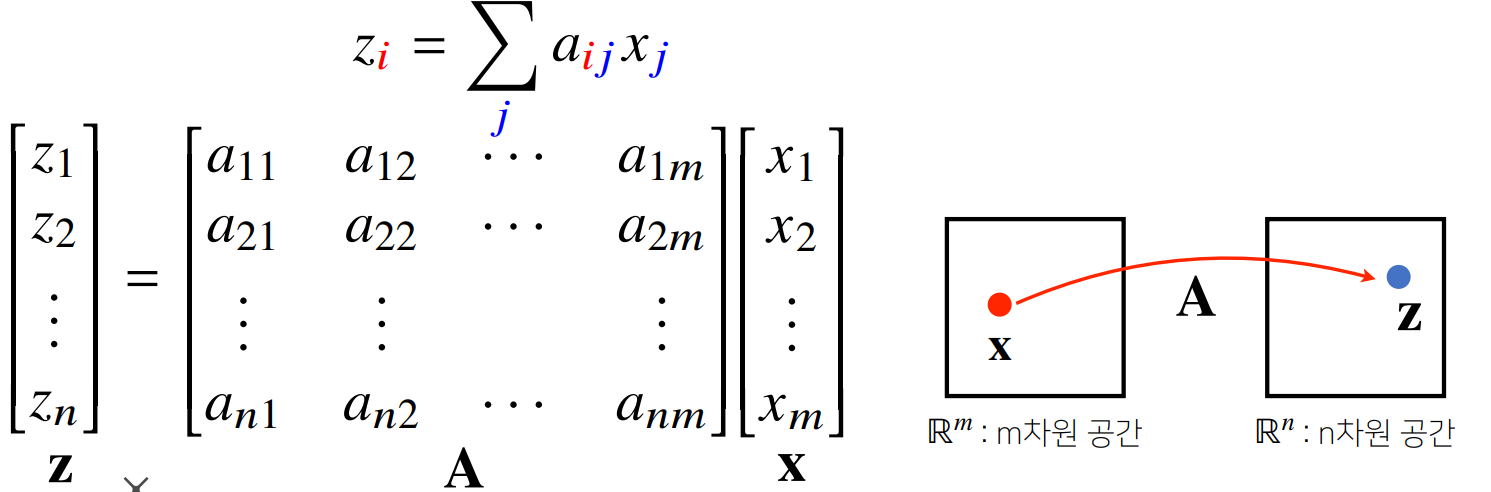
모든 선형변환(linear transform)은 행렬곱으로 계산할 수 있다

역행렬(inverse matrix)이란

  • 행렬 A의 연산을 거꾸로 돌리는 행렬 (A^(-1))
  • 행과 열 숫자가 같고 행렬식(determinant)가 0이 아닌 경우에만 계산 가능

 

 

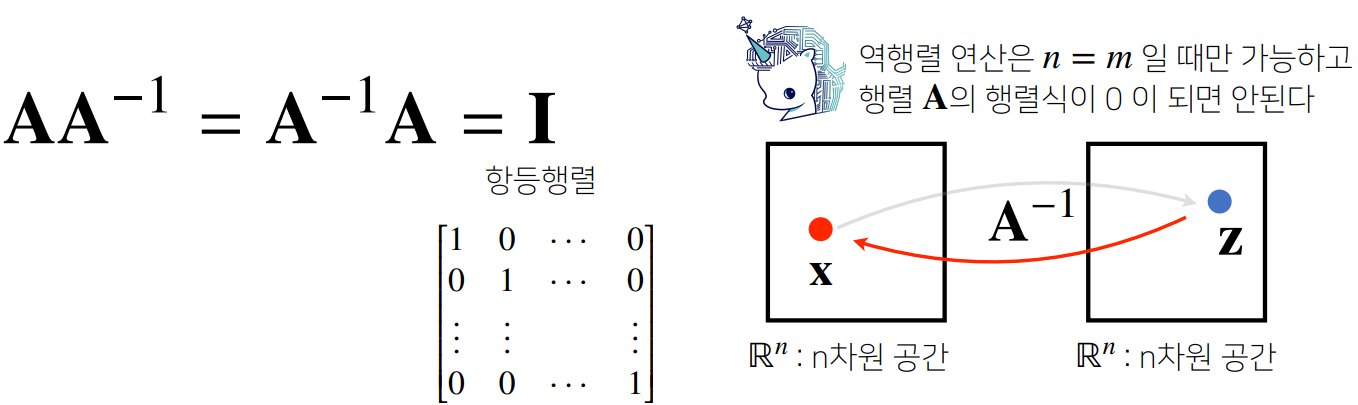
항등행렬(identity matrix) : 임의의 벡터나 행렬을 곱했을 때 자기 자신이 나오는 행렬

행렬식: 어떤 특별한 계산식에 따라 행렬의 원소들을 대입하여 얻은 결과값(수치)을 지칭한다 (즉, 행렬에 대해 계산되는 하나의 숫자값이다). 다만 그 결과값이 그 행렬의 특성을 결정짓는 중요한 값이기에 determinant라 부른다.

 

 

linear algebra의 inv 사용      np.linalg.inv()

x= np.array([[1,-2,3],
            [7,5,0],
            [-2, -1, 2]])

np.linalg.inv(x) #역행렬 구하기
'''
array([[ 0.21276596,  0.0212766 , -0.31914894],
       [-0.29787234,  0.17021277,  0.44680851],
       [ 0.06382979,  0.10638298,  0.40425532]])
'''
x@ np.linalg.inv(x) 
'''
array([[ 1.00000000e+00, -1.38777878e-17,  0.00000000e+00],
       [ 0.00000000e+00,  1.00000000e+00,  0.00000000e+00],
       [-2.77555756e-17,  0.00000000e+00,  1.00000000e+00]])
'''

 

역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어펜로즈(Moor-Penrose) 역행렬 A^(+)를 이용한다

np.linalg.pinv()

 

n은 행, m은 열을 뜻함

 

행이 열보다 크면 유사역행렬을 원래 행렬보다 먼저 곱해줘야 항등행렬이 나옴

x= np.array([[0,1],
            [1,-1],
            [-2, -1]])

np.linalg.pinv(x) 
'''
array([[-0.07142857,  0.28571429, -0.35714286],
       [ 0.35714286, -0.42857143, -0.21428571]])
'''

응용 1) 연립방정식 풀기: 변수의 개수가 식의 개수보다 많은 경우

 

 

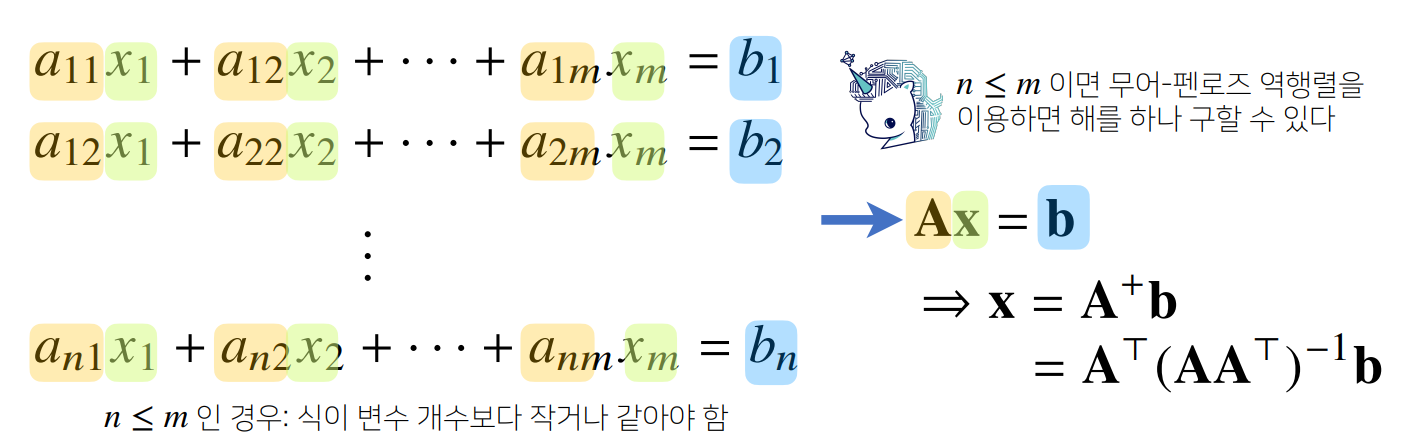
중학교 수학) 식의 개수와 변수의 개수가 같아야 해를 구할 수 있음

 

 

응용 2) 선형회귀분석 : 식의 개수가 변수의 개수보다 많은 경우

 

어떤 베타를 써야 빨간색 점을 잘 표현하는 선형모델을 찾을 수 있을까

 

 

y를 만족하는 X를 찾는 건 불가능. X가 주어진 상태에서 베타를 찾아야함

 

 

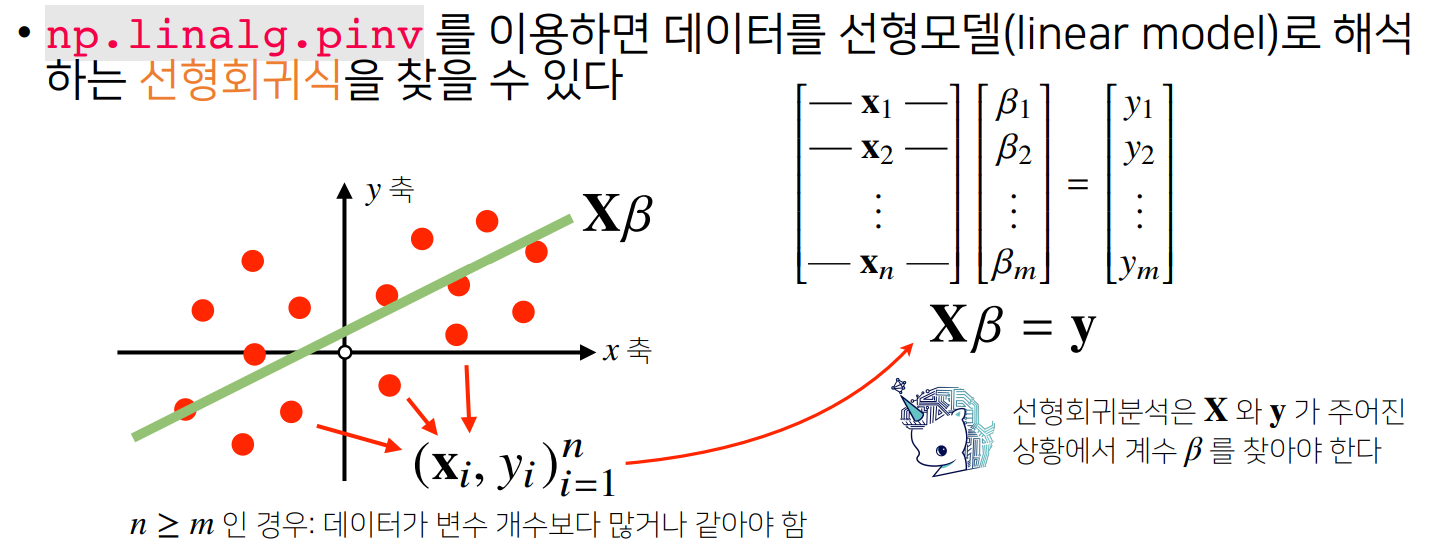
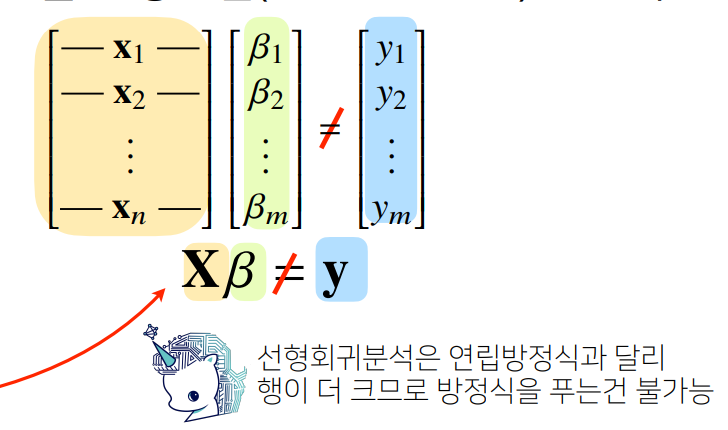
우리가 찾은 선형모델식: y hat