[matplotlib] Line Plot
<목차>
- Line Plot이란
- 원칙
- 실습
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as pltLine Plot이란
- 연속적으로 변화하는 값을 점으로 나타내고 이를 선으로 연결한 그래프로, 꺾은 선 그래프, line chart, line graph 등으로 불림
- bar plot은 .bar()을 사용하지만 line plot은 .line()이 아닌 .plot()을 사용함
- Noise의 인지 방해를 줄이기 위해 smoothing을 사용함
- Line을 구별하는 요소는 세 가지
(1) 색상 (2) 마커 (3) 선의 종류: solid, dashed, dashdot, dotted, None
fig, ax = plt.subplots(1, 1, figsize=(5, 5))
np.random.seed(97) #seed 고정
x = np.arange(7)
y = np.random.rand(7)
ax.plot(x, y,
color='black',
marker='*',
linestyle='solid',
)
plt.show()
line plot은 왼쪽에서 오른쪽으로 그리는 게 일반적이지만
문법 자체는 이전 점 (x1,y1) 에서 (x2,y2) 로 잇고, (x2,y2) 에서 (x3,y3) 로 잇는다.
-> 정N각형이나 원을 그릴 수 있음
fig, ax = plt.subplots(1,1, figsize=(5,5))
n = 1000
x = np.sin(np.linspace(0, 2*np.pi, n)) #(시작점, 끝점, 간격)
y = np.cos(np.linspace(0, 2*np.pi, n))
ax.plot(x, y)
plt.show()
fig = plt.figure(figsize=(5, 5))
ax = fig.add_subplot(111, aspect=1) # 비율을 1로함
n = 1000
x = np.sin(np.linspace(0, 2*np.pi, 4)) #(시작점, 끝점, 간격)
y = np.cos(np.linspace(0, 2*np.pi, 4))
ax.plot(x, y)
plt.show()
[tip]
1. 추세
- bar plot과 다르게 꼭 축을 0부터 시작할 필요 없음
- 때로는 구체적인 line plot보다 생략된 것이 나을 수 있음
생략되지 않는 선에서 범위를 조정하여 변화율 관찰 (.set_ylim())
# Ax1
ax1 = fig.add_subplot(121)
ax1.plot(x, y,
marker='o',
linewidth=2)
ax1.xaxis.set_major_locator(MultipleLocator(1)) # 그리드 생성
ax1.yaxis.set_major_locator(MultipleLocator(0.05))
ax1.grid(linewidth=0.3)2. 간격
- 규칙적인 간격을 사용해야 함. 아니면 자칫 혼동을 줌
- 규칙적인 간격의 데이터가 아니라면 각 관측값에 점을 표시하자 (ex. x축 간격은 1,5,10,15..인데 데이터는 x가 2,4,11일때)
x = [2, 3, 5, 7, 9]
y = [2, 3, 4, 7, 10]
fig, ax = plt.subplots(1, 3, figsize=(13, 4))
ax[0].plot([str(i) for i in x], y)
ax[1].plot(x, y)
ax[2].plot(x, y, marker='o')
plt.show()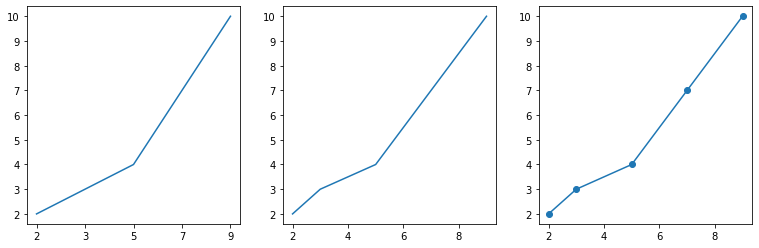
3. 보간
- 알려진 지점의 값 사이(중간)에 위치한 값을 알려진 값으로부터 추정하는 것 -> 없는 데이터를 있다고 혼동시킬 수 있으므로 지양
- 데이터의 error나 noise가 포함되어 있는 경우, 데이터의 이해를 돕는 방법
o Moving Average
o Smooth Curve with Scipy
o scipy.interpolate.make_interp_spline()
o scipy.interpolate.interp1d()
o scipy.ndimage.gaussian_filter1d()
from scipy.interpolate import make_interp_spline, interp1d
import matplotlib.dates as dates
fig, ax = plt.subplots(1, 2, figsize=(20, 7), dpi=300)
date_np = google.index
value_np = google['close']
date_num = dates.date2num(date_np)
# smooth
date_num_smooth = np.linspace(date_num.min(), date_num.max(), 50)
spl = make_interp_spline(date_num, value_np, k=3)
value_np_smooth = spl(date_num_smooth)
# print
ax[0].plot(date_np, value_np)
ax[1].plot(dates.num2date(date_num_smooth), value_np_smooth)
plt.show()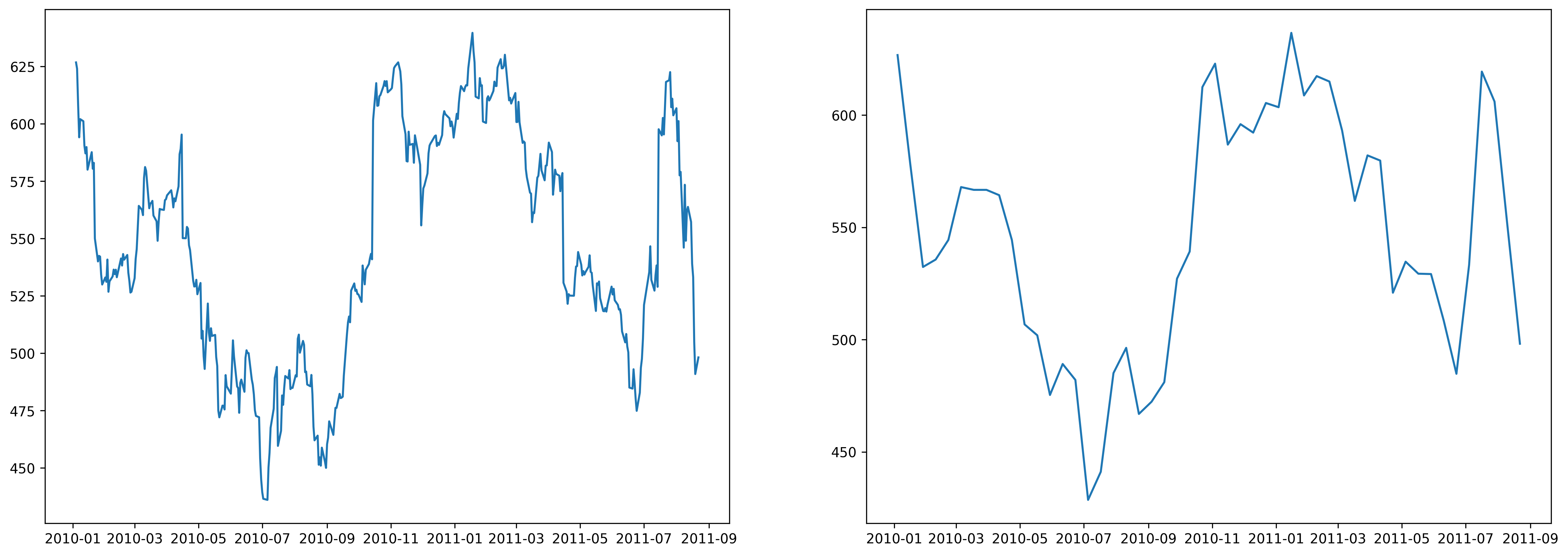
4. 이중축
- 축이 두 개 필요 .twinx()
- 한 데이터에 대해 다른 단위 (ex. radian과 degree)로 표현하는 경우 -> 이 외 지양
.secondary_xaxis(), .secondary_yaxis()
fig, ax1 = plt.subplots(figsize=(12, 7), dpi=150)
# First Plot
color = 'royalblue'
ax1.plot(google.index, google['close'], color=color)
ax1.set_xlabel('date')
ax1.set_ylabel('close price', color=color)
ax1.tick_params(axis='y', labelcolor=color)
# # Second Plot
ax2 = ax1.twinx()
color = 'tomato'
ax2.plot(google.index, google['volume'], color=color)
ax2.set_ylabel('volume', color=color)
ax2.tick_params(axis='y', labelcolor=color)
ax1.set_title('Google Close Price & Volume', loc='left', fontsize=15)
plt.show()
def deg2rad(x):
return x * np.pi / 180
def rad2deg(x):
return x * 180 / np.pi
fig, ax = plt.subplots()
x = np.arange(0, 360)
y = np.sin(2 * x * np.pi / 180)
ax.plot(x, y)
ax.set_xlabel('angle [degrees]')
ax.set_ylabel('signal')
ax.set_title('Sine wave')
secax = ax.secondary_xaxis('top', functions=(deg2rad, rad2deg)) #위쪽 변
secax.set_xlabel('angle [rad]')
plt.show()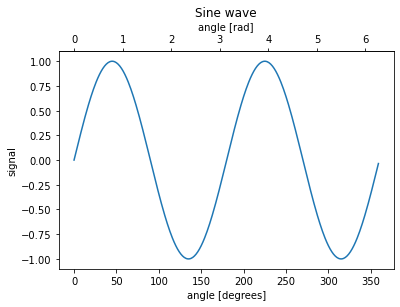
5. etc
- 범례대신 레이블 추가
- 주석: min/max 정보를 annotation으로
- 신뢰구간, 분산 등의 uncertainty는 연한색으로 표현
fig = plt.figure(figsize=(12, 5))
x = np.linspace(0, 2*np.pi, 1000)
y1 = np.sin(x)
y2 = np.cos(x)
# Ax2
ax = fig.add_subplot(111, aspect=1)
ax.plot(x, y1,
color='#1ABDE9',
linewidth=2,)
ax.plot(x, y2,
color='#F36E8E',
linewidth=2,)
# text를 어떻게 쓸 수 있는가!
ax.text(x[-1]+0.1, y1[-1], s='sin', fontweight='bold',
va='center', ha='left',
bbox=dict(boxstyle='round,pad=0.3', fc='#1ABDE9', ec='black', alpha=0.3))
ax.text(x[-1]+0.1, y2[-1], s='cos', fontweight='bold',
va='center', ha='left',
bbox=dict(boxstyle='round,pad=0.3', fc='#F36E8E', ec='black', alpha=0.3))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.show()
fig = plt.figure(figsize=(7, 7))
np.random.seed(97)
x = np.arange(20)
y = np.random.rand(20)
ax = fig.add_subplot(111)
ax.plot(x, y,
color='lightgray',
linewidth=2,)
ax.set_xlim(-1, 21)
# max
ax.plot([-1, x[np.argmax(y)]], [np.max(y)]*2,
linestyle='--', color='tomato'
)
ax.scatter(x[np.argmax(y)], np.max(y),
c='tomato',s=50, zorder=20)
# min
ax.plot([-1, x[np.argmin(y)]], [np.min(y)]*2,
linestyle='--', color='royalblue'
)
ax.scatter(x[np.argmin(y)], np.min(y),
c='royalblue',s=50, zorder=20)
plt.show()
실습을 위한 데이터 준비하기
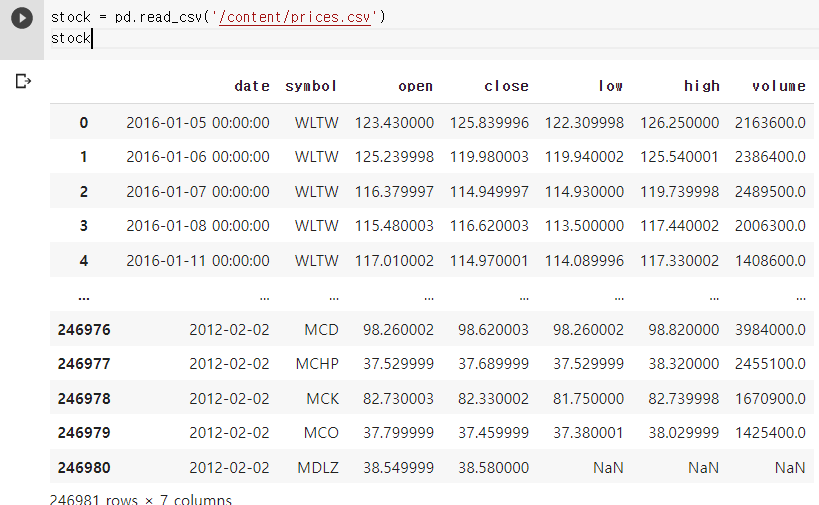
stock['date'] = pd.to_datetime(stock['date'], format='%Y-%m-%d', errors='raise')
stock.set_index("date", inplace = True)
stock
# FAANG
apple = stock[stock['symbol']=='AAPL']
google = stock[stock['symbol']=='GOOGL']
google.head()
rolling을 사용해 이동평균 사용하기
google_rolling = google.rolling(window=20).mean()
fig, axes = plt.subplots(2, 1, figsize=(12, 7), dpi=300, sharex=True)
axes[0].plot(google.index,google['close'])
axes[1].plot(google_rolling.index,google_rolling['close'])
plt.show()
