AI TECH

Regularization 규제

prefer_all 2022. 10. 5. 13:49
<목차>
  • Early stopping
  • Parameter norm penalty
  • Data augmentation : Data set 늘리기
  • Noise robustness
  • Label smoothing
    Mixup, Cutout, CutMix
  • Dropout
  • Batch normalization

 

Regulation이란

- Generalization이 잘 되도록 학습에 반대되도록 규제를 건다. (학습을 방해함으로써 학습 데이터에만 잘 동작되는 게 아니라 test data에도 잘 작동되도록)

 

왜 Regulation을 사용하는 가

- 딥러닝은 알고리즘 특성상 복잡도가 높아 과적합이 발생하기 쉽다. 과적합 문제를 해결하기 위해 여러 가지 정규화(Regularization) 방법이 요구되었다.

 

  • Early stopping

Training error와 validation error 사이의 차이가 커지면 training을 멈추자

Validation data가 필요한 방법

 

 

 

  • Parameter norm penalty

cost func에 parameter norm penalty을 추가하여 파라미터 값에 제약을 줌으로써 모델의 복잡도를 낮춘다

add smoothness to the function space

 

NN parameter가 너무 커지지 않게 함

(ex. network paramer을 전부 다 제곱해서 더하면 나오는 수를 줄임)

이왕이면 network를 학습할 때 network weight 숫자가 (크기의 관점에서) 작으면 작을 수록 좋다

 

부드러운 함수일 수록 generalize performance가 높을 것이라는 가정이 있음

 

 

 

  • Data augmentation

Label이 변하지 않는 한에서 Data set 늘리기

more datas are always welcomed

 

 

 

  • Noise robustness

add random noises inputs or weights

입력 데이터와 weight에 noise를 넣음

이유는 모름

 

 

 

  • Label smoothing

Data augmented와 유사함. 학습데이터 두 개를 뽑아서 섞어줌. 

효과: 일반적으로 분류 문제를 풀 때 decision boundary를 찾고자 할 때, decision boundary를 부드럽게 해줌

두 개의 이미지를 고르고 label과 이미지를 모두 섞음

 

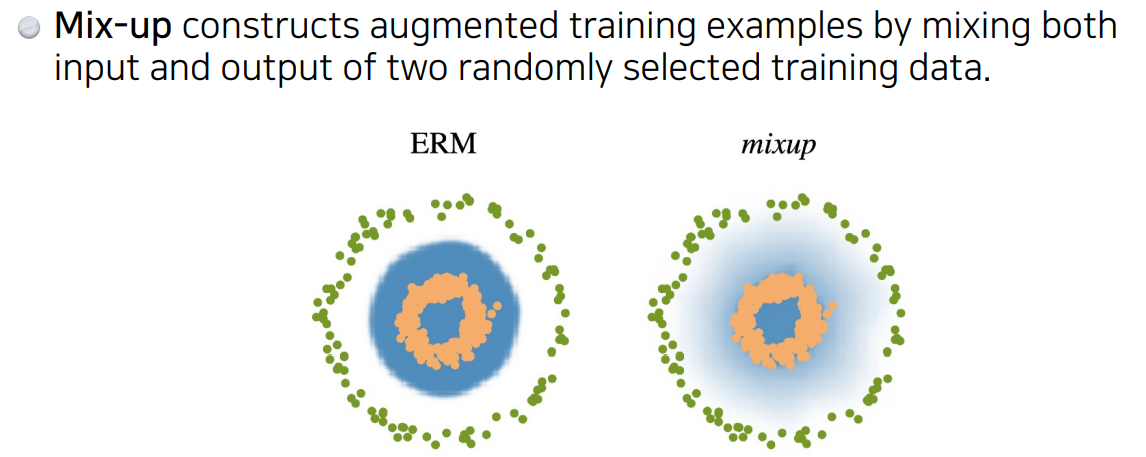
cutout: 이미지의 일정 영역을 빼줌

blending 하는 게 아니라 특정영역은 dog, cat

 

 

  • Dropout

In each forward pass, randomly set some neurons to zero

 

NN의 weight를 0으로 바꿈

장점: 각 뉴런이 robust한 feature로 잡을 수 있다

 

 

Gradient Vanishing / Exploding 문제

신경망에서 학습시 Gradient 기반의 방법들은 파라미터 값의 작은 변화가 신경망 출력에 얼마나 영향을 미칠 것인가를 기반으로 파라미터 값을 학습시키게 된다.
만약 파라미터 값의 변화가 신경망 결과의 매우 작은 변화를 미치게 될 경우 파라미터를 효과적으로 학습 시킬 수 없게 된다. Gradient 라는 것이 결국 미분값, 즉 변화량을 의미하는데 이 변화량이 매우 작아지거나(Vanishing) 커진다면(Exploding) 신경망을 효과적으로 학습시키지 못하고, Error rate 가 낮아지지 않고 수렴해버리는 문제가 발생하게 된다.   

그래서 이러한 문제를 해결하기 위해서 Sigmoid 나 tanh 등의 활성화 함수들은 매우 비선형적인 방식으로 입력 값을 매우 작은 출력 값의 범위로 squash 해버리는데, 가령 sigmoid는 실수 범위의 수를 [0, 1]로 맵핑해버린다.
이렇게 출력의 범위를 설정할 경우, 매우 넓은 입력 값의 범위가 극도로 작은 범위의 결과 값으로 매핑된다.
이러한 현상은 비선형성 레이어들이 여러개 있을 때 더욱 더 효과를 발휘하여 학습이 악화된다. 첫 레이어의 입력 값에 대해 매우 큰 변화량이 있더라도 결과 값의 변화량은 극소가 되어버리는 것이다.

그래서 이러한 문제점을 해결하기 위해 활성화 함수로 자주 쓰이는 것이 ReLU(Rectified Linear Unit) 이다. 또한 아래와 같은 방법들도 존재한다.   
1) Change activation function : 활성화 함수 중 Sigmoid 에서 이 문제가 발생하기 때문에 ReLU 를 사용
2) Careful initialization : 가중치 초기화를 잘 하는 것을 의미
3) Small learning rate : Gradient Exploding 문제를 해결하기 위해 learning rate 값을 작게 설정함  

위와 같은 트릭을 이용하여 문제를 해결하는 것도 좋지만, 이러한 간접적인 방법 보다는 "학습하는 과정 자체를 전체적으로 안정화"하여 학습 속도를 가속 시킬 수 있는 근본적인 방법인 "배치 정규화(Batch Normalization)"를 사용하는 것이 좋다. 이는 위와 마찬가지로 Gradient Vanishing / Gradient Exploding이 일어나는 문제를 방지하기 위한 아이디어이다.

출처

 

  • Batch normalization

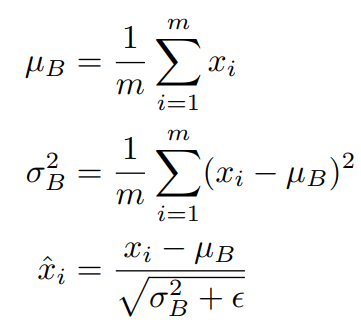
Batch normalization compute the empirical mean and variance independently for each dimension (layers) and normalize

 

내가 적용하고자 하는 layer의 statistics를 정교화시킴. 평균과 분산을 조정하는 과정이 신경망 안에 포함되어 학습시 값이 조정됨.

즉, 각 layer마다 정규화하는 layer을 두어 변형된 분포가 나오지 않도록 조절하는 것임

 

효과: internal covariace shift를 줄인다 (많은 다른 논문들이 동의하지 않음)

 

이 논문에서는 학습에서 불안정화가 일어나는 이유를 Internal covariance shift라고 주장하는데,
이는 네트워크의 각 layer나 activation마다 입력값의 분산이 달라지는 현상을 뜻한다.

- Covariate Shift : 이전 레이어의 파라미터 변화로 인하여 현재 레이어의 입력의 분포가 바뀌는 현상
- Internal Covariate Shift : 레이어를 통과할 때 마다 Covariate Shift 가 일어나면서 입력의 분포가 약간씩 변하는 현상

 

한가지 확실한 건 layer을 깊게 쌓을 때 batch normalization을 사용하면 성능이 올라감

 

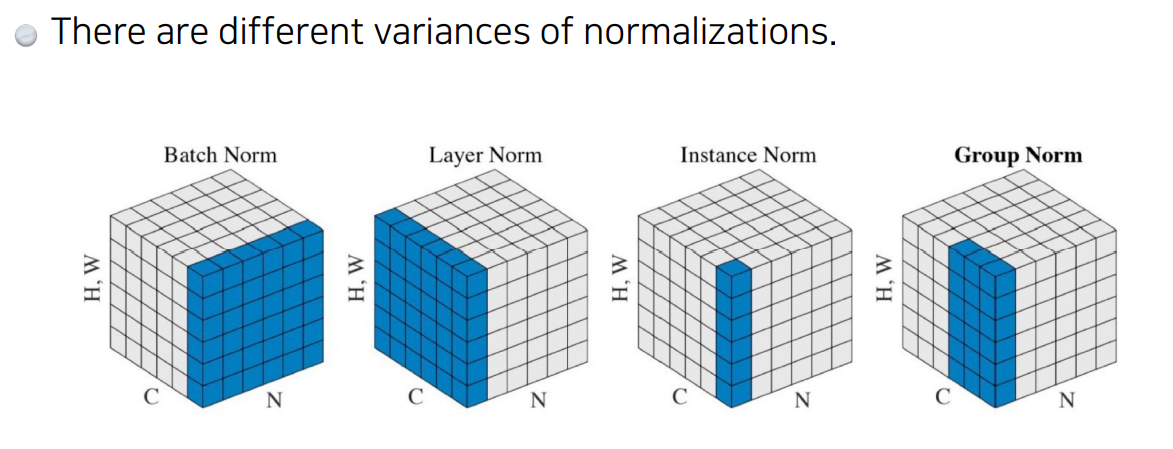
왜 잘되는 지 해석하기 보다는 활용해보면 효율이 좋다고 이해