Logistic Regression

https://wikidocs.net/57805

<목차>
- Binary Classification(이진분류)
- Sigmoid function
- Cost function
- pytorch로 구현

 

인공신경망으로 표현되는 Logistic regression

화살표: 입력과 곱해지는 가중치나 편향 / 출력하기 전에 sigmoid함수를 지남

---

Sigmoid function

• S자 모양의 그래프를 그릴 수 있음

• 선형회귀와 마찬가지로 최적의 W와 b를 찾는 게 목표
• Sigmoid 출력값은 0과 1 사이의 값을 가짐 -> 분류작업에 사용가능
  • ex) 임계값을 0.5: 출력값이 0.5 이상이면 1(True), 0.5이하면 0(False)으로 판단
• W값 변화에 따른 경사도의 변화: W값이 커지면 (파란색 그래프처럼) 경사가 커짐

%matplotlib inline
import numpy as np 
import matplotlib.pyplot as plt

def sigmoid(x): # 시그모이드 함수 정의
    return 1/(1+np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(0.5*x)
y2 = sigmoid(x)
y3 = sigmoid(2*x)

plt.plot(x, y1, 'r', linestyle='--') # W의 값이 0.5일때
plt.plot(x, y2, 'g') # W의 값이 1일때
plt.plot(x, y3, 'b', linestyle='--') # W의 값이 2일때
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()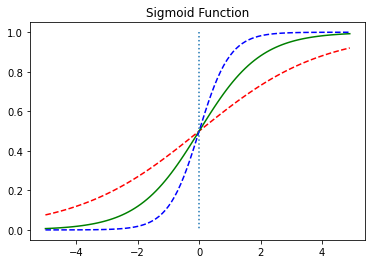

 

• b값 변화에 따른 좌, 우 이동: b값이 클수록 좌측으로 이동

x = np.arange(-5.0, 5.0, 0.1)
y1 = sigmoid(x+0.5)
y2 = sigmoid(x+1)
y3 = sigmoid(x+1.5)

plt.plot(x, y1, 'r', linestyle='--') # x + 0.5
plt.plot(x, y2, 'g') # x + 1
plt.plot(x, y3, 'b', linestyle='--') # x + 1.5
plt.plot([0,0],[1.0,0.0], ':') # 가운데 점선 추가
plt.title('Sigmoid Function')
plt.show()

---

Cost function

 

아래와 같은 선형 회귀에서 사용했던 평균 제곱 오차의 수식에서

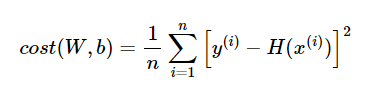
이제 H(x) = Wx + b가 아니라 H(x) = sigmoid(Wx+b)임. 그래서 이 cost func를 미분하면 비볼록(non-convex) 형태의 그래프가 나옴

경사하강법의 문제: 오차가 최소값이 되는 구간에 도착했다고 판단해도 실제로 오차가 최소값인 구간이 아닐 수 있음 -> Global minimum에 도달해야함

 

(해결) log 함수를 사용하자

sigmoid func의 출력값은 0과 1 사의 값임

실제값이 1이면 주황색 그래프. 실제값이 0이면 초록색 그래프

이 비용함수에 대해 경사하강법을 수행하면서 최적의 가중치 W를 찾아감

---

pytorch로 구현

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

torch.manual_seed(1)

# 훈련 데이터 선언
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data) #torch.Size([6, 2])
y_train = torch.FloatTensor(y_data) #torch.Size([6, 1])

# 가중치 벡터와 편향 선언
W = torch.zeros((2, 1), requires_grad=True) # 크기는 2 x 1
b = torch.zeros(1, requires_grad=True)

# optimizer 설정
optimizer = optim.SGD([W, b], lr=1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    # 가설 설정
    hypothesis = torch.sigmoid(x_train.matmul(W) + b)
    # hypothesis = 1 / (1 + torch.exp(-(x_train.matmul(W) + b))) 위와 동일 
    
    # Cost 계산
    cost = -(y_train * torch.log(hypothesis) + 
             (1 - y_train) * torch.log(1 - hypothesis)).mean()

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

이제 W와 b는 훈련 후의 값을 가지고 있음

현재 W와 b를 가지고 예측값을 출력해보자

hypothesis = torch.sigmoid(x_train.matmul(W) + b)
print(hypothesis)
'''
tensor([[2.7648e-04],
        [3.1608e-02],
        [3.8977e-02],
        [9.5622e-01],
        [9.9823e-01],
        [9.9969e-01]], grad_fn=<SigmoidBackward>)
'''

위 값들은 0과 1 사이의 값임. 이제 0.5를 넘으면 True, 넘지 않으면 False로 

 

prediction = hypothesis >= torch.FloatTensor([0.5])
print(prediction)
'''
tensor([[False],
        [False],
        [False],
        [ True],
        [ True],
        [ True]])
'''

실제 값과 동일하게 예측한 것 확인 가능

 

 

nn.module로 구현

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

torch.manual_seed(1)

# 훈련 데이터 선언
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0], [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data) #torch.Size([6, 2])
y_train = torch.FloatTensor(y_data) #torch.Size([6, 1])

# 모델 설정 ******
model = nn.Sequential(
   nn.Linear(2, 1), # input_dim = 2, output_dim = 1
   nn.Sigmoid() # 출력은 시그모이드 함수를 거친다
)

# optimizer 설정 ******
optimizer = optim.SGD(model.parameters(), lr=1)

nb_epochs = 1000
for epoch in range(nb_epochs + 1):

    # 가설 설정
    hypothesis = model(x_train)
    
    # Cost 계산 ******
    cost = F.binary_cross_entropy(hypothesis, y_train)

    # cost로 H(x) 개선
    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    # 100번마다 로그 출력
    if epoch % 10 == 0:
        prediction = hypothesis >= torch.FloatTensor([0.5]) # 예측값이 0.5를 넘으면 True로 간주
        correct_prediction = prediction.float() == y_train # 실제값과 일치하는 경우만 True로 간주
        accuracy = correct_prediction.sum().item() / len(correct_prediction) # 정확도를 계산
        print('Epoch {:4d}/{} Cost: {:.6f} Accuracy {:2.2f}%'.format( # 각 에포크마다 정확도를 출력
            epoch, nb_epochs, cost.item(), accuracy * 100,
        ))

 

 

Class로 pytorch 모델 구현하기

model = nn.Sequential(
   nn.Linear(2, 1), # input_dim = 2, output_dim = 1
   nn.Sigmoid() # 출력은 시그모이드 함수를 거친다
)

class BinaryClassifier(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(2, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        return self.sigmoid(self.linear(x))